Normal dağılım, aritmetik ortalama etrafında standart sapmaya bağlı olarak verilerin düzgün bir şekilde dağılımını modellemek için kullanılır. Örneğin, bir ülkenin nüfusunun yaş dağılımı veya bir toplumun IQ ölçüm sonuçları gibi veriler normal dağılım gösterebilir.
Örnek olarak bir popülasyona ait IQ Skor ölçümlerinin normal dağılım gösterdiğini varsayalım. Ölçüm sonuçlarının ortalamasının 100 ve standart sapmasının da 15 olduğunu görebilirsiniz.
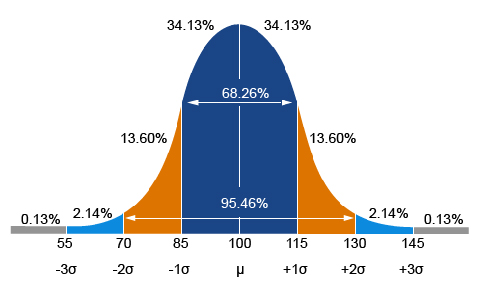
Elimizdeki örnekleme göre ana kitlenin %68 inin IQ skoru: 85 ile 115 arasındadır veya %95'i 70–130 puanları arasında yer almıştır diyebiliriz.
- Aritmetik ortalamanın 1 standart sapma altında ve üstündeki aralık, tüm verinin %68'lik kısmını temsil etmektedir.
- Aritmetik ortalamanın 2 standart sapma altında ve üstündeki aralık, tüm verinin %95'lik kısmını temsil etmektedir.
- Aritmetik ortalamanın 3 standart sapma altında ve üstündeki aralık, tüm verinin %99'luk kısmını temsil etmektedir.
Bu dağılımın özelliklerini şu şekilde sıralayabiliriz.
- Aritmetik ortalama, mod ve medyan birbirine eşittir.
- Eğrinin maksimum noktası aritmetik ortalamadır.(dolayısıyla mod ve medyandır).
- Eğri aritmetik ortalamaya göre simetriktir.
- Çarpıklık (skewness) katsayısı normal dağılımda 0'dır.
- Basıklık (kurtosis) katsayısı da normal dağılımda 0'dır.






